Lights off(关灯游戏)终极算法

xiaoee posted @ 2009年2月23日 12:24 in I am Thinking with tags flash 算法游戏 Mathematica , 22035 阅读

关灯游戏是一个十分有趣的智力游戏，它的规则是：有h行l列的方格子(所谓的灯），游戏开始时有个初始状态，当你点击其中一盏灯，它和它的紧邻上下左右( 对于位于中间的灯，它的紧邻上下左右共有4盏灯，角上的灯的紧邻只有 2盏灯，边上非角上的灯的紧邻为3盏灯)的灯的状态将全部改变，原来是灭的灯变亮，原来亮的灯则变灭，要求游戏玩家设法将全部的灯变成事先规定的终止状态。
该游戏流行的玩法是：初始局面随机确定一些灯是亮的，另外的是灭的，按照上面的规则，要求玩家设法将全部的灯关掉。这里有一个。

由于对一个格子点两次等于没有点，所以所以我们只要找出h*l处格子哪些需要被点一下，这样有2^(h*l)种情况，我们显然可以这样来设计一个程序穷举所有的情况，看是否符合终止状态。可以想像这种算法的效率是很低的。

进一步，我们把初始状态表示成一个hl*1的0-1矩阵P，终止状态也表示成一个hl*1的0-1矩阵F，单独点每i个格子产生的的变化也可以表示成一个hl*l的0-1矩阵di，Ki表示第i个格子是否被点，则游戏过程可表示成P+Sum(Ki*di)=F,Sum(Ki*di)=(d1,d2,d3...dhl).(K1,K2,K3...Khl)^T=D.K,这样问题就是解一个矩阵方程：D.K=F-P。下面是在Mathematica上计算的一个例子，初始状态为空：

n = 5;(*下面生成文章中的 D 矩阵，这里用的nn*)
nn = Table[If[i == j, 1, 0], {i, 1, n*n}, {j, 1, n*n}];
For[i = 1, i <= n*n, i++,
p = Floor[(i - 1)/n] + 1;
q = Mod[i - 1, n] + 1;
If[p + 1 <= n, nn[[p*n + q, i]] = 1, 1 == 1;];
If[p - 1 > 0, nn[[(p - 2)*n + q, i]] = 1, 1 == 1;];
If[q + 1 <= n, nn[[(p - 1)*n + q + 1, i]] = 1, 1 == 1;];
If[q - 1 > 0, nn[[(p - 1)*n + q - 1, i]] = 1, 1 == 1;];];
(*F就是终止状态*)
F = {0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0,
1, 0, 0};
LinearSolve[nn, F, Modulus -> 2]

结果：

{0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1,0, 0}

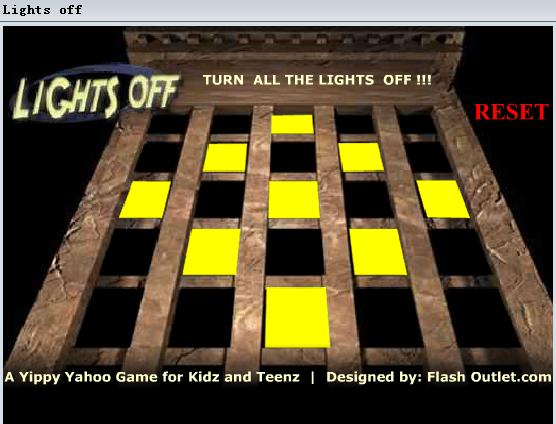
其实上面的结果可以在一个5*5的格子上生成最上面图片上那种情况。

这种算法的效率也不是最高的，但它可以对任何初始状态和终止状态的情况做出计算。

我们还可以进一步发现其实如果我们一行一行的点，当第一行点完后，第二行也就确定了因为你不可能让第一行的灯关掉，否则它不可能再被打开，这样你的工作就是确定第一行的点法，再在第二行把第一行亮的关掉，依次完成下面的每一行。这样需要穷举的情况就变成了2^Min(h,l)了。根据这个想法我在Mathematica上面完成了代码：

For[h = 5; l = 5; i = 0, i < 2^h, i++,
n = 2^^1101110101010101010111011;
For[j = 0, j < h, j++,
If[BitGet[i, j] == 1,
c = BitSet[0, j];
a = If[Mod[j, h] == 0, 0, BitSet[0, j - 1]];
d = If[Mod[j + 1, h] == 0, 0, BitSet[0, j + 1]];
w = 0;
s = If[j/h >= l - 1, 0, BitSet[0, j + h]];
n = BitXor[n, c, a, s, d, w], 1 == 1;]];
For[j = h, j < h*l, j++,
If[BitGet[n, j - h] == 0,
w = BitSet[0, j - h];
c = BitSet[0, j];
a = If[Mod[j, h] == 0, 0, BitSet[0, j - 1]];
d = If[Mod[j + 1, h] == 0, 0, BitSet[0, j + 1]];
s = If[j/h >= l - 1, 0, BitSet[0, j + h]];
n = BitXor[n, c, a, s, d, w], 1 == 1;]];
If[n == 2^(h*l) - 1, Print[BaseForm[i, 2]], 1 == 1;]]

结果：

100(2)
1010(2)
10001(2)
11111(2)

上面的结果其实就是整个结果编码的低位。

在第一行(依据初始编码的顺序，为低位的第一行)运用上面的结果，再完成下面的各行就可以把灯全部灭掉。

其中h，l分别为行数和列数，n为初始状态，用二进制编码：要达到的状态用1这里是关，消除的状态用0这里是开。

这种算法很快，但是只能处理终止状态为(满或者说空的情况，注意到代码中的n==2^(h*l)-1。)

我看到的网上的各种这样的游戏都是给出初始状态，要你将灯全部关掉或者打开，都可以用这种算法。这里还有一个。