Apr 10
Mar 28
在提出「生成函数」的数学定义之前，我们先考虑几个简单的排列组合问题。(不知道怎么回事，发表这篇文章首页显示会有问题，搞了好久没找到问题，于是清空重新输入了一遍，并把所有公式都去掉了，用文本代替，首页显示终于没问题了，可能公式就得你费力看了）。
考虑恒等式：(1+ax)(1+bx)(1+cx)=1+(a+b+c)x+(ab+bc+ac)x^2+abcx^3
如将a,b,c 看作代表三个对象，它的右边是一多项式，其系数恰代表了将 a,b,c 作组合的各种可能。常数项1表示在三对象中一个都不取；x 的系数a+b+c 表示在a,b,c 中取一个的各种组合，即或取a，或取b，或取 c；x^2 的系数ab+bc+ac 表取二个的各种组合；x^3之系数表示了三个皆取的唯一方法。在这里可能产生各种情形是用+号连接，同时发生之事件则用乘法（即符号并列）表示。
又设有5个球 a,a,a,b,c，其中三个球a 完全一样，则恒等式：
(1+ax+a^2x^2+a^3x^3)(1+bx)(1+cx)= 1+(a+b+c) x+(a^2+a b+a c+b c) x^2+(a^3+a^2 b+a^2c+
a b c) x^3+(a^3 b+a^3 c+a^2 b c) x^4+a^3 b c x^5
其中 x^r的系数表示了选取r个的各种可能组合(1<=r<=5 )。
在排列组合问题中，加法原则与乘法原则是大家熟知的两个法则。加法原则是讲如一事件可能发生情况有 m 种，另一种事件可能发生情况有 n 种，则这两种事件其一发生情况有m+n 种。乘法原则是讲如一事件可能发生情况有m种，另一事件可能发生情况有n种，则这两事件同时发生情况有mn种。我们在上面两例用到的是一种符号运算，它遵从这两法则。在第二个例子中，因子(1+ax+a^2x^2+a^3x^3)表示了或不取a，或取一个a，或取2个a，或取三个a 的各种情况；而在第一个例子中，(1+ax)(1+bx)表示了如果 a , b 被允许同时选取时可能产生之各种情况。
Mar 10
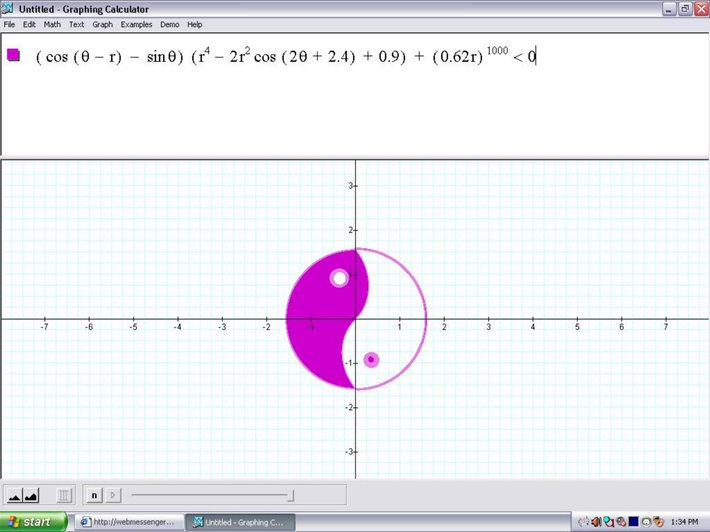
在M67的博客上发现了这张图。由于Mathematica里没有画极坐标隐函数的函数，所以他上面只写了一个Free Pascal的程序。我研究了一下，终于用Mathematica画出了上面一样的图形。像下面这样：
Mar 10
我今天构造一个这样一个不等式：
0.5 < Mod[Int[T*2^(-8 Int[x] - Mod[Int[y], 8])，2]
其中：T＝202486808888363389480137910375037701804044605404484441980698178。
它生成的图像竟然是下面这个样子：
你一定会觉得很神奇，这样的函数是怎么构造出来的呢？仔细想一下，你会发现其实这一点也不难，知道怎么回事后你也可以做出像这样的式子来。
