最近学习编译原理,正在学习文法,书上提到0型方法的描述能力相当于图灵机,
于是想验证一下,既然是相当于图灵机,那么应该可以仅通过方法规则来进行运算。。
我就来定义了一个二进制加法器:
P:
A->A0 | A1 | e
A+e->A
e+A->A
A0+A0->A+A0
A0+A1->A+A1
A1+A0->A+A1
A1+A1->A+A+10
如果我们要从111+11+1推导出1011
可以像这样: 111+11+1=>111+1+e+10
=>111+1+10
=>111+e+e+100
=>111+e+100
=>111+100
=>11+101
=>1+111
=>e+e+1011
=>e+1011
=>1011
下面是我用python写的一个简单实现该转换的程序:
今天翻看以前的日记,看到几个月前发现的一个斐波那契数列的递推公式: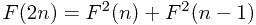 (公式二)
(公式二)
在这里Fibonacci数列为从0开始的这样一个序列:1,1,2,3,5,8,13,21 . . .,满足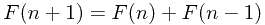 ,n>0;
,n>0;
记得当时是在晚上睡觉的时候在想怎么把递归程序转换成非递归程序的时候,想到Fibonacci数列,然后就想到上面那个公式的。
看到这个公式,还真不知道当时是怎么想出来的,于是把以前的草稿纸都翻了一下,才终于找到怎么推导出来的(看来有了想法一定要记录下来才行啊),如下:
问:(x - a)(x - b)(x - c) . . . (x - z)=?,给你5秒钟。。。
解答:你一定已经知道了,就是0啦。 (x - a)(x - b)(x - c) . . . (x-x)(x-y)(x - z)
请注意(x-x),哈哈!!!!
井字游戏,英文名是tic-tac-toe,最原始是游戏是在一个3*3的方格棋盘中,每人轮流下看谁先连成横竖或斜着一条线就算赢了,我们把种线叫做tic-tac-toe线,可以在这里http://allaboutfrogs.org/funstuff/java/tictactoe/玩一下这个游戏。现在我们问的是如果是在一个n*n*n的立方体中玩这个游戏,有多少种tic-tac-toe线?比如对于3*3*3的方块,横竖的情况有27种,在面上斜对角的情况有18种,体对角的情况有4种,所以一共有27+18+4=49种。
解答_证明:
其实这是一道很简单的题,如果用上面的常规做法显然没什么意思,下面看一个另类的做法:
找出一个10位数,使它的第i位(从左到右数,最左边为第0位)上的数等于i在整个数中出现的次数。比如,8000000010,它有8个0,1个8,但不它不该有1。
解答:
如果第0是9,其它的9个位就都必须是0了,所以这种情况不行。
如果第0位上是8,那么其它9个位有一个不是0,很明显,每8位必须有个1,但是这样的话,每一位得有个1,0就不是8个了。所以这种情况也不行。
如果每0位上是7,这样第7位上需要一个1,所以第一位要一个1,这样就有两个1了,所以第一位要一个2,这样第2位就必须是1了,所有数字的和超过10了。
让我们试试把6放在第0位,这样第6位需要一个1,还是一样第一位要一个1,这样就得到两个1,所以我们放个2在第一位,再在第2位放上1,这样就OK了。
所以我们要是数就是:6210001000。

找出方程(6x - 1)(3x - 1)(2x - 1) = 4 的实根。
解答: 令y=6x,则方程变成:
(y - 1)(y/2 - 1)(y/3 - 1) = 4
或者:
(y - 1)(y - 2)(y - 3) = 2*3*4
很明显上面方程的唯一实根就是y=5,所以x=y/6=5/6。
这样一来,我们可以反过来构造许多这样的方程了。