3435363738394041424344454647484950515253545556575859606162636465666768
69707172737475767778798081828384858687888990919293949596979900010203...
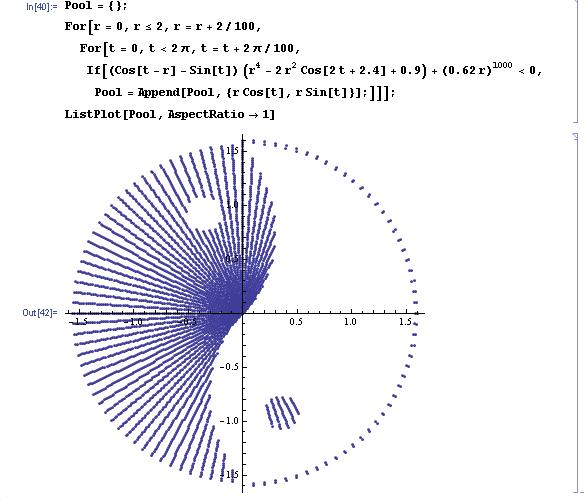
可能是用这种方法式子中有大量的三角函数运算,所以很浪费时间,而上篇文章中的那种方法巧妙的把大部分三角函数去掉了,所以特别的快。
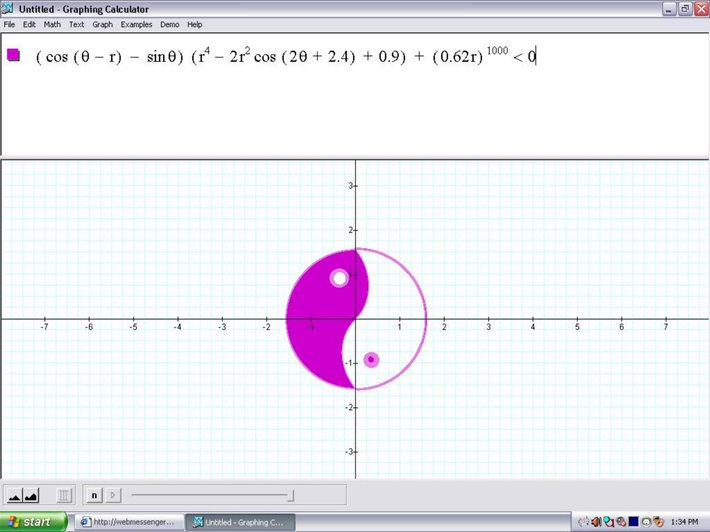
在M67的博客上发现了这张图。由于Mathematica里没有画极坐标隐函数的函数,所以他上面只写了一个Free Pascal的程序。我研究了一下,终于用Mathematica画出了上面一样的图形。像下面这样:
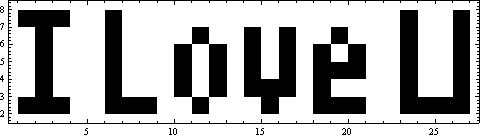
你一定会觉得很神奇,这样的函数是怎么构造出来的呢?仔细想一下,你会发现其实这一点也不难,知道怎么回事后你也可以做出像这样的式子来。
昨天我们上英语课,老师问我们一个问题:如果一个精灵承诺你三个愿望,你会许什么愿望?
有的人说想成为百万富翁,有的人说想变成明星,竟然有一个说想要好多美女做老婆的。
一听到这个问题我就想起了一个搞笑的对上帝不是万能的证明:如果上帝是万能的,那请他创造出一个他自己也举不起来的石头,要是上帝造不出来,显然上帝就是万能的,要是他造出来了,他举不起来,也证明上帝不是万能的。
当老师问到我时,我说:我首先想知道精灵你是否能实现我一切的愿望。
如果他说是,那么我接着说:
我想让你告诉我一个你不能实现的愿望。
如果他说不出,很显然第一个问题你在骗我,如果他真的说出了一个,他还是在骗我。
如果他说不是,那他对我的承诺就是假的。
最后我对老师说,精灵在骗人,他可能不能实现我全部的三个愿望。
我又说,虽然这样,精灵还是可以实现我很多愿望的,既然我至少还有一次机会,我希望精灵再承诺我三个愿望。
老师无语。。。
利用1,3,9克的砝码和一架天平,0到13克整数重量就都可以被称出来了,在下面的Flash中循环显示了这14种重量是怎样被称量的,注意在这个过程中,每一步都只增加或拿下一个砝码。
如果再增加一个27克的砝码,则0到40克的整数重量也都可以被称出来了,存在像上面那样的41步的一个循环吗,它称出所有41种重量,而每一步都只增加或拿下一个砝码?