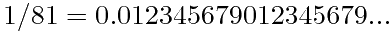Module77:Yes,it is.

Mar 12

奇妙的循环数字序列

Mathematics 0 Comments

1/9801=

0.00010203040506070809101112131415161718192021222324252627282930313233
3435363738394041424344454647484950515253545556575859606162636465666768
69707172737475767778798081828384858687888990919293949596979900010203...

这是一个有198位循环结的循环小数。

其实要制造这样的分数并不难，难的是找到这样形式简单的，比如我用Mathematica找了一个这样的：

13717421/1111111111＝

0.0123456789012345678901234567890123456789...

我是在这个网站上看到的，你可以在上面进行分数和小数的转换，可以算出分数是有限的还是循环的，并可以给出循环结。可以在这个网站上进行这类有趣分数序列的探索，不过好像计算能力不算强，像我上面这个0-9的循环就算不出来。

Feb 12

祖冲之的密率355/113的精妙

Mathematics 2 Comments

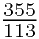祖冲之的密率 $$\frac{355}{113}$ ，这个密率的妙处，在于它的分母不大而精确度很高？在所有分母不超过113的分数当中，和 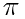$$\pi$ 最接近的就是 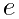$$\frac{355}{113}$ 。不但如此，华罗庚在《数论导引》中用丢番图理论证明，在所有分母不超过336的分数当中，和PI最接近的还是 $$\frac{355}{113}$ 。后来在夏道行教授所著《 $$\pi$ 和》一书中，用连分数的方法证明，在所有分母不超过8000的分数当中，和 $$\pi$ 最接近的仍然是 $$\frac{355}{113}$ ,大大改进了336这个界限。有趣的是，只用初中里学的不等式的知识，竟能把8000这个界限提高到16500以上！