Module77:Yes,it is.

问：(x - a)(x - b)(x - c)  . . .  (x - z)＝？，给你5秒钟。。。

解答：你一定已经知道了，就是0啦。 (x - a)(x - b)(x - c)  . . .  （x-x)(x-y)(x - z)

           请注意（x-x)，哈哈！！！！

找出一个10位数，使它的第i位（从左到右数，最左边为第0位）上的数等于i在整个数中出现的次数。比如，8000000010，它有8个0,1个8,但不它不该有1。
 
解答：
    如果第0是9,其它的9个位就都必须是0了，所以这种情况不行。
    如果第0位上是8,那么其它9个位有一个不是0,很明显，每8位必须有个1,但是这样的话，每一位得有个1,0就不是8个了。所以这种情况也不行。
    如果每0位上是7,这样第7位上需要一个1,所以第一位要一个1,这样就有两个1了，所以第一位要一个2,这样第2位就必须是1了，所有数字的和超过10了。
    让我们试试把6放在第0位，这样第6位需要一个1,还是一样第一位要一个1,这样就得到两个1,所以我们放个2在第一位，再在第2位放上1,这样就OK了。
    所以我们要是数就是：6210001000。

找出方程(6x - 1)(3x - 1)(2x - 1) = 4 的实根。

解答：                                         令y＝6x，则方程变成：

(y - 1)(y/2 - 1)(y/3 - 1) = 4

                                                                              或者：

(y - 1)(y - 2)(y - 3) = 2*3*4

    很明显上面方程的唯一实根就是y＝5,所以x＝y/6=5/6。

    这样一来，我们可以反过来构造许多这样的方程了。

设n为整数，如果式子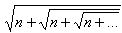：表示一个整数，证明：n为两个连续整数的乘积。

证明：设整数T为式子表示的整数，那么t^2=n+t,即t^2-t-n=0，t=[1+-Sqrt(1-4n)]/2，那么1-4n＝r^2,

           可以看出r为奇数，所以n=(r^2-1)/4=[(r-1)/2][(r+1)/2]，这样就证明了n为两个连续整数的乘积。

能否找到五个连续的整数，使前面的四个数的四次方之和等于最后一个数的四次方？

解答：也许你用Mathematica算出很长一个表达式，显然不是整数。事实确实是找不到，证明很简单：我们考虑下一个数的四次方被5除的余数，可以只看这几个数5k,5k+1,5k+2,5k+3,5k+4,可以看出余数分别是0,1,1,1,1。这样当把前前4个余数起来只能是3或4,这样就证明了无解了。

求b，使得在b进制下35(b)和58(b)互质（即最大公约数是1）。

解答：显然b>=9,因为58中含有数字8。我们知道35(b)=3*b+5,58(b)=5*b+8。假设d是它们的任意一个公约数。则d整除5*35(b)-3*58(b)=5*(3*b+5)-3*(5*b+8)=1。

所以d一定整除1,这样d＝1。所以35(b)和58(b)在任何其底b>=9下都互质。