Feb 22

分数维简介

Mathematics 0 Comments

     我们平常所听说的维数，或者维数都是对空间的，比如一个点是0维的，一条直线是1维的，一个平面是2维的，一个立体是3维的,这种维数符合庞加莱在1912年提出的维数的拓扑定义，并且——十分合理地——按此定义得到的维数总是整数。但还有一种维数定义，可以得到分数维，也称豪斯道夫-贝斯可维奇维数。这种维数概念最初是由豪斯道夫(Felix Hausdorff)在1919年提出的，并且在后来由贝斯可维奇加以发展，这就是它名字的由来。
    分数维是怎样定义的呢？通过对下面标度维数的说明可以体会到分数维数。
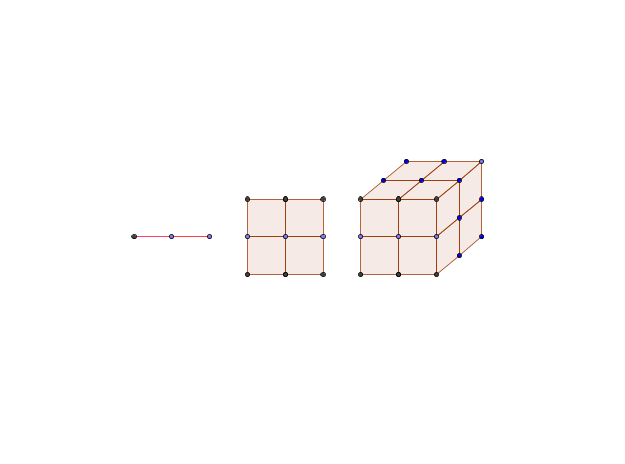
我们知道某些形状相同的几何体放在一起可以组成一个较大的它们的复制品。例如，需要2条相同的线段（1维的）组成长度扩大到两倍的一条线段。需要4个相同的正方形（2维几何体）组成棱长扩大到两倍的一个正方形。需要8个相同的正方体组成一个边长扩大到2倍的一个正方体。

Feb 10

超球面和超球体

Mathematics 0 Comments

n维超立方体的体积很简单，即边s的n次方：$s^n。

 

那n维超球的体积又是怎么样的呢？

 

首先，我们定义一些概念。圆周是2维圆盘的1维边界（界限）。球面是3维球体的2维表面（界限）。超球面（n维球面）和超球（n维球体）可以有不同的维数。普通的球面是2维球面。普通球体是3维球体。圆周也可以被称为1维球面。圆盘也可以被叫作2维球体。