Mar 28
设n为整数,如果式子: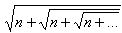 表示一个整数,证明:n为两个连续整数的乘积。
表示一个整数,证明:n为两个连续整数的乘积。
证明:设整数T为式子表示的整数,那么t^2=n+t,即t^2-t-n=0,t=[1+-Sqrt(1-4n)]/2,那么1-4n=r^2,
可以看出r为奇数,所以n=(r^2-1)/4=[(r-1)/2][(r+1)/2],这样就证明了n为两个连续整数的乘积。
设n为整数,如果式子: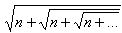 表示一个整数,证明:n为两个连续整数的乘积。
表示一个整数,证明:n为两个连续整数的乘积。
证明:设整数T为式子表示的整数,那么t^2=n+t,即t^2-t-n=0,t=[1+-Sqrt(1-4n)]/2,那么1-4n=r^2,
可以看出r为奇数,所以n=(r^2-1)/4=[(r-1)/2][(r+1)/2],这样就证明了n为两个连续整数的乘积。
2009年3月3日被全球不少数学迷称作“平方根节”(Square Root Day),一些地区数学迷开展形式多样的庆祝活动。
每逢“平方根节”,月份和日期的数字正好是当年最后两位数字的平方根。这一节日每个世纪只出现9次,对数学迷而言相当珍贵。有人把块根类蔬菜切成正方体以示庆祝,有人则把食物制成根号模样。
美国加利福尼亚州教师罗恩·戈登特意举办一场小型竞赛,获胜者可得339美元的奖励。戈登说:“这些日子(平方根日)就像日历中的彗星。人们等啊等,它们点亮你的生活后又突然消失。”
上一个“平方根节”出现在2004年2月2日。要想庆祝下一个“平方根节”,数学迷需等到7年后的2016年4月4日。