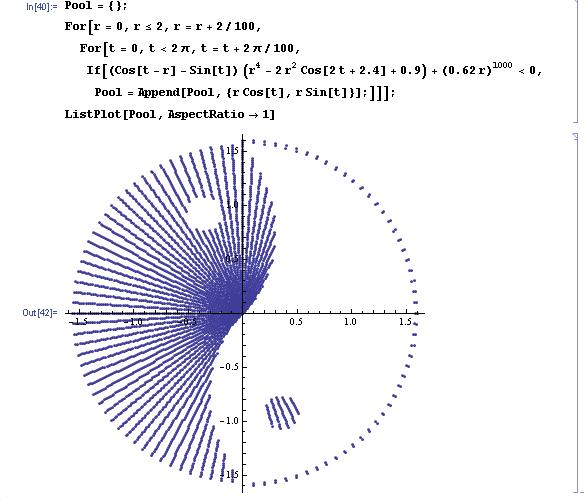
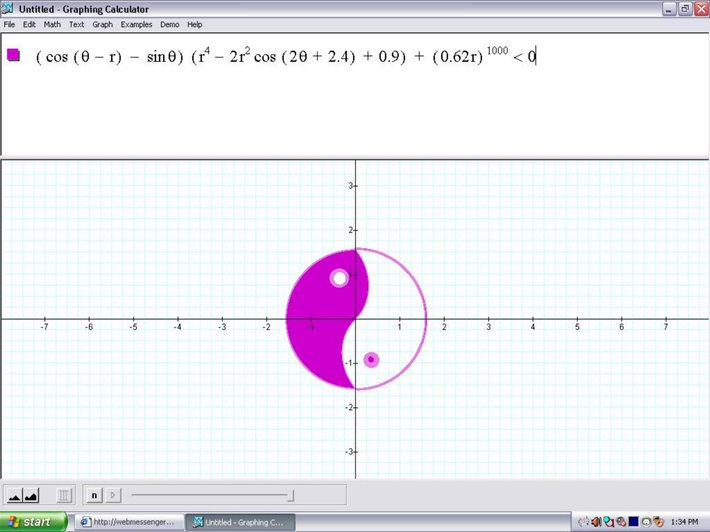
Apr 8
在一个大圆中,四个半径为大圆一半的小圆过圆心分布在坐标轴的x,y轴正负半轴上,如图:
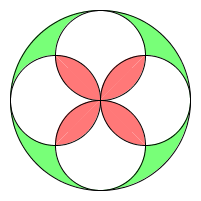
证明小圆两两相交的面积之和(红色区域)和小圆没有覆盖的面积(绿色区域)相等?
先看一个外国人怎么证明的:
证明:先考虑上面图形的1/8,并给各个面积标上a,b,c,d等,如下图:
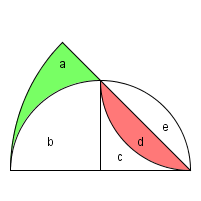
设R是大圆的半径,我们可以得到:
a+b+c+d=PI*R*R/8;
b+c+d+e=PI*R*R/8;
这样就得到a=e=d;8a=8d,这样就证明了。