奇妙的数字序列
也许你看过这样的：
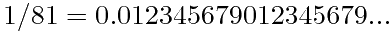
但你不一定看过这样的：
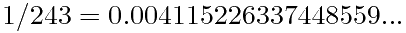
这个系列会怎样继续？243这个数学有什么特别呢？（你可以把它因式分解看看）是什么原因造成这样
的序列的？在其它的基底下有和这个相似的数吗？1/243=0.00411522633744855967078189300411...这样循环下去。
有理数是形如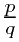
（其中p,q为整数，q不等于0）的数，它们都可以表示成无限循环小数。
比如：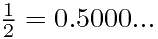
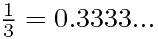
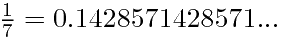
为什么会这样呢？
想想我们做竖式除法的过程，在这过程上每次必有一个非零的余数，否则这进位小数是有限的,可以
表示成无限0循环。并且这所有的余数将是1和q-1之间的整数，所以最多最多只能有q-1个不同的余数
值，这意味着，最多除q次，某个余数k将第二次出现。但由此随后而来的所有余数，将按照余数k第一
次出现后它们出现的同样次序重复。
那怎样确定无限循环小数所对应的分数形式呢？
一般的我们是把那个小数表示成某个常数和无穷等比级数的和：
比如：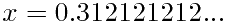
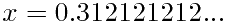
我们有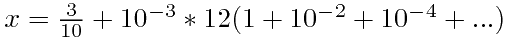
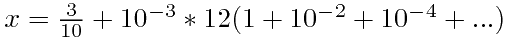
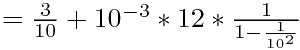
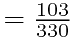
另外一种方法是这样的：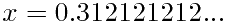
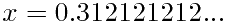
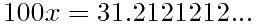
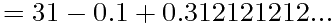
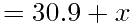
从而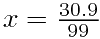 
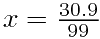
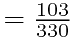
用上面的任一种方法都容易证明：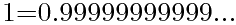
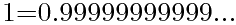
这样: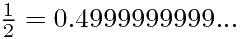 
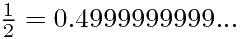
最后我们发现数142857有如下性质：用数2,3,4,5,6中的任一个去乘它，所得的积只是它的数码的重新排列。
你可以试着用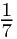
的十进位小数展开式来解释。
参考：《什么是数学》
评论 (0)
