Module77:Yes,it is.
Eureka...
xiaoee
search
分类
热门文章
最新评论
随机文章
最新留言
标签云
ArchLinux
C语言
Fibonacci
LXDE
Love
MM
Mathematica
NASM
OS
PI
QQ
Windows7
Wolfram
YY
blog
boot
bug
cs
csdn
firefox
flash
fun
github
gmail
grub
hyde
javascript
kernel
linux
loader
python
quine
vim
vista
win7
上帝
二进制
互质
人体
人工智能
人生
代码
位运算
体积
信号灯
倒霉
公式
写作
几何
函数
分层
分形
分数
分析
分类
初等
博客
历史
反思
发散
可变参数
周易
器官
回文
图像
图形
图片
圆周率
声明
大学生
大牛
天平
太极图
奇妙
女孩
妙解
学习
定理
审查
密率
封装
小数
左手鼠标
平方根
广告
序列
库函数
循环
心情
心理
心理学
快捷键
思考
总结
恋爱
恶作剧
情书
愤怒
愿望
我爱你
抽象
排列
排序
控制论
推理
搜索引擎
搞笑
操作系统
收敛
故事
数值计算
数列
数学归纳法
数论
文法
方法
方程
无敌
无法睡眠
无限
日期
易经
曲线
最值
极坐标
每日一题
测试
游戏
灰色
物理
特征值
特征函数
生成函数
生日
生活
生物
画图
睡眠
硬件
祖冲之
科研
积分
程序
程序员
空间
算法
精灵
级数
组合
维度
编程
编辑器
网站
网络
美女老师
翻译
自我指涉
自指
自由
节日
英语
计划
计算
计算机科学
设计
证明
诗
调和
趣题
过滤
近似
进制
递归
递推
邮箱
隐函数
难题
面向对象
面积
面试
高维
魔方
链接
存档
计数器
608052
CNZZ
Welcome Here.
The Bottom..
你喜欢这儿吗?
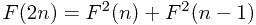 (公式二)
(公式二)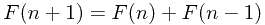 ,n>0
,n>0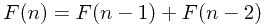
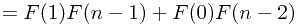
![$=F(1)[F(n-2)+F(n-3)]+F(0)F(n-2) $=F(1)[F(n-2)+F(n-3)]+F(0)F(n-2)](/user_files/Module77/epics/00550def75fbb58f2f38b7b75cea4b18b68296b7.png)
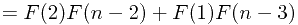

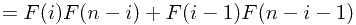 , n>0 (公式一)
, n>0 (公式一)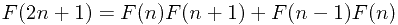
![=F(n)[F(n+1)+F(n-1)] =F(n)[F(n+1)+F(n-1)]](/user_files/Module77/epics/0ea8c3c7790bbb13d1d6d55d79dc71376be691d4.png)
![=F(n)[F(n)+2F(n-1)] =F(n)[F(n)+2F(n-1)]](/user_files/Module77/epics/6aeb005fcb2430a95e739fcaf114278cbcea0380.png)
 评论 (0)
评论 (0)