用数学归纳法证明任意两个正整数相等

xiaoee posted @ 2009年2月08日 05:30 in Mathematics with tags fun 数学归纳法 , 4955 阅读

首先证明A(n):a,b是使max(a,b)=n成立的任意两个正整数，则a=b.

证明：a)假设A(r)成立；设a,b是任意两个使得max(a,b)＝r+1的正整数。

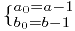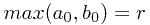考虑两个整数 $\{^{a_0=a-1}_{b_0=b-1}$ , 则 $max(a_0,b_0)=r$ ,又由于我们假设A(r)成立，

因此 $a_0=b_0$ ，由此知 $a=b$ 。因此A(r+1)成立。

b)A(1)显然成立。因为如果max(a,b)=1成立，则由于a,b假设是正整数，则 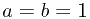$a=b=1$ 。因此按数学归纳法A(n)对所有的正整数成立。

max(1,2)=2,所以1＝2.

这样就可以得出任意两个正整数相等了。

事实上数学归纳法的两个要点是：

a)对任一正整数r,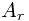 $A_r$ 为真时能推出 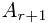$A_{r+1}$ 也为真；

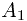b)已知 $A_1$ 为真。

在用数学归纳法时，我们必须经常确保条件a）和b）是真正被满足的。

上面错误的原因是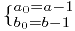 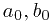$\{^{a_0=a-1}_{b_0=b-1}$ , $a_0,b_0$ 可能已经不是正整数了，不满足a）。

Module77:Yes,it is.