历时半个世纪的一道平面几何难题
证明:任给平面上不全共线的n>=3个点,一定存在恰好通过其中两个点的直线。
刚看到这到题的时候还真不知道怎么动手,从两个点开始加点构造,似乎也找不到
明显的规律,看来正面构造是不行的,那反过来构造所有直线都通过至少两个点的情况,
试了半天也找不到,而且也是随着点的增加越来越复杂,怎么办呢?这也难怪解决它花
其实这是在1893年开始流传的一道平面几何难题,看起来并不难,但历时40多年才
被人证明。从下面介绍的证明方法看它其实是一道很简单的几何问题(我觉得它可能和
我们印象中的几何题可能很不一样啊!),竟能困惑数学家如此之久,真是不可思议。
证明是出奇的简单而巧妙。对平面上给定的n个不共线的点,过其中的任意两点作直
线L。因为所给的点不全在同一条直线上,所以L外必有其他的给定点。记L外的点a到L的
距离为p(a,L)。由于所给的定点只有n个,过其中任意两点也只能作有限条直线,因此
仅有有限多个距离p(a,L),从而有通过某两个点的直线L0以及L0外的某个定点a0使得
距离p(a0,L0)最小。下面将证明L0就是所求的直线,亦即L0上恰好有两个给定的点。
如果L0不是,设三个不同的定点a1,a2,a3在直线L0上。从a0做到L0的垂线,高相应
如果L0不是,设三个不同的定点a1,a2,a3在直线L0上。从a0做到L0的垂线,高相应
的垂足为点h(见图)。//图画得不好,请见谅。

此时三个定点a1,a2,a3中至少有两个点在垂足h的同一侧(包含与h重合的情况),
不妨设a1和a2在h的同侧,且a1位于h和a2之间。现在,过a0和a2作直线L1。显然点a1不
在直线L1上,并且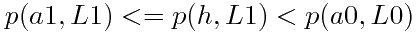 ,矛盾,
,矛盾,
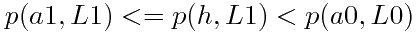 ,矛盾,
,矛盾,因为已知p(a0,L0)是最小的。这就证明了直线L0恰好通过两个给定的点。
参考来源:《数学的100个基本问题》
 评论 (0)
评论 (0)