超球面和超球体
n维超立方体的体积很简单,即边s的n次方: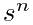 。
。
那n维超球的体积又是怎么样的呢?
首先,我们定义一些概念。圆周是2维圆盘的1维边界(界限)。球面是3维球体的2维表面(界限)。超球面(n维球面)和超球(n维球体)可以有不同的维数。普通的球面是2维球面。普通球体是3维球体。圆周也可以被称为1维球面。圆盘也可以被叫作2维球体。
n维容量是几何形体的n维“体积”。比如:
圆周的1维容量是它的周长,
圆盘的2维容量是它的面积,
球面(2维)的2维容量是它的表面积,
球体(3维)的3维容量是它的体积,
3维超球面的3维容量是它的超表面积,
4维超球体的4维容量是它的4维超体积。
下面的表格显示出不同维度的超球体的n维容量(体积)和它们对应的超球面的边界(n-1维)容量(超表面积):
|
维度 (n) |
整体形 |
整体形n维容量(“体积”) |
边界形 |
边界形n-1维容量(“表面积”) |
|
2 |
圆盘 (2维) |
π r2 |
圆周 (1维) |
2π r |
|
3 |
球体 (3维) |
(4/3)π r3 |
球面 (2维) |
4π r2 |
|
4 |
4维超球体 |
(1/2)π2r4 |
3维超球面 |
2π2r3 |
|
5 |
5维超球体 |
(8/15)π2r5 |
4维超球面 |
(8/3)π2r4 |
|
6 |
6维超球体 |
(1/6)π3r6 |
5维超球面 |
π3r5 |
|
7 |
7维球体 |
(16/105)π3r7 |
6维球面 |
(16/15)π3r6 |
很奇怪,为什么每次维数增加2,π的指数才增加1?
一般的,n维超球体的n维容量(“体积”)是:
|
当n为偶数: |
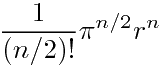 |
|
当n为奇数: |
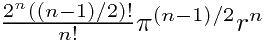 |
Or 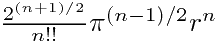 |
这里n! = n(n-1)(n-2)... (阶乘),n!! = n(n-2)(n-4)... (双阶乘)。
一般的,n维超球体的边界表面积(n-1维容量)等于“体积”(n维容量)乘以(n/r)。其实你可以通过n维超球的“体积”(n维容量)对半径求导数得到它的超表面积(n-1维容量)。同样对n维超球对应的边界形的表面积(n-1维容量)对r在(0,r)上求积分可以得到n维超球的体积。
 评论 (0)
评论 (0)