祖冲之的密率355/113的精妙
祖冲之的密率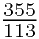 ,这个密率的妙处,在于它的分母不大而精确度很高?在所有分母不超过113的分数当中,和
,这个密率的妙处,在于它的分母不大而精确度很高?在所有分母不超过113的分数当中,和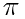 最接近的就是
最接近的就是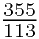 。不但如此,华罗庚在《数论导引》中用丢番图理论证明,在所有分母不超过336的分数当中,和PI最接近的还是
。不但如此,华罗庚在《数论导引》中用丢番图理论证明,在所有分母不超过336的分数当中,和PI最接近的还是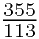 。后来在夏道行教授所著《
。后来在夏道行教授所著《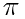 和
和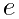 》一书中,用连分数的方法证明,在所有分母不超过8000的分数当中,和
》一书中,用连分数的方法证明,在所有分母不超过8000的分数当中,和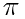 最接近的仍然是
最接近的仍然是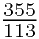 ,大大改进了336这个界限。有趣的是,只用初中里学的不等式的知识,竟能把8000这个界限提高到16500以上!
,大大改进了336这个界限。有趣的是,只用初中里学的不等式的知识,竟能把8000这个界限提高到16500以上!
根据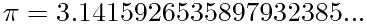 ,
,
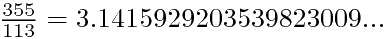 ,
,
可得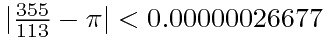 ,如果有个分数
,如果有个分数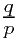 比
比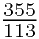 更接近
更接近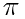 ,
,
一定会有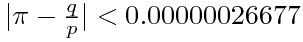 ,
,
于是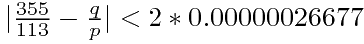 ,
,
也就是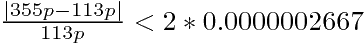
因为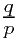 不等于
不等于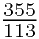 ,所以|355p-113q|不为0.但它是正整数,大于或等于1,
,所以|355p-113q|不为0.但它是正整数,大于或等于1,
所以 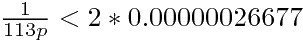
由此推出

这表明如果有个分数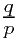 比
比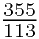 更接近
更接近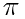 ,其分母p一定大于16586.
,其分母p一定大于16586.
如此简单初等的推理得到这样好的成绩,可谓鸡刀宰牛。
事实上以上得到界限已经快到极限了,下面是我用Mathematica计算的代码和结果:
For[i = 16500, i < 16650, i++,
For[j = Ceiling[3.14159 i], j <= 3.14193 i, j++,
If[Abs[j/i - Pi] <= 355/113 - Pi, Print[j/i], 1 == 1;]]]
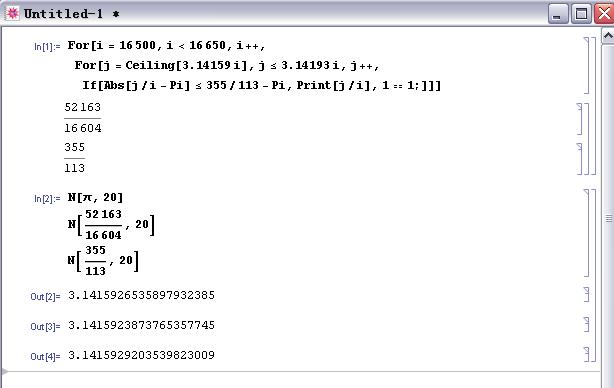
从结果可以看出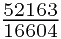 就比
就比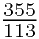 更接近
更接近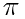 ,看来16603是这个极限。
,看来16603是这个极限。
参考来源:《进位制与数学游戏》
《好玩的数学系列》
2009年2月12日 11:01
你好誇張,
355 / 113 = 2.6691729323308270677 ???
2009年2月13日 05:47
@獨立的圓:不好意思,忘打省略了。。谢谢提醒 ,已改正了。
,已改正了。