函数图像竟然是我爱你
xiaoee
posted @ 2009年3月10日 08:42
in Mathematics
with tags
函数 图像 Mathematica 我爱你 证明 二进制 位运算 自指
, 10240 阅读
我今天构造一个这样一个不等式:
0.5 < Mod[Int[T*2^(-8 Int[x] - Mod[Int[y], 8]),2]
其中:T=202486808888363389480137910375037701804044605404484441980698178。
它生成的图像竟然是下面这个样子:
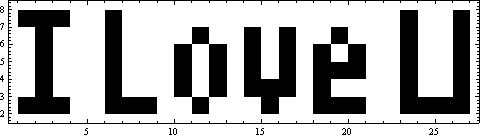
你一定会觉得很神奇,这样的函数是怎么构造出来的呢?仔细想一下,你会发现其实这一点也不难,知道怎么回事后你也可以做出像这样的式子来。
在上面的式子里,变量x和y都加上了取整符号,因此整个图象将是一格一格的。于是不等式右边就简化为T * 2^( -8x - y mod 8) mod 2,其中x和y都取整数。我们知道,一个数乘以2的负k次方相当于对应的二进制数右移k位,那么T * 2^(-k) mod 2实质上就是二进制数T右起第k位上的数字。其实T是以下2进制数:
0111111000000010000000100111111000000000000000000001101000101010000111
1000000000001111000000011000111100000000000001110000100010000111000000
00000000001000000010011111100000000000000000010000100111111001000010
也就是"I Love U"的像素点的一个编码。以下是我在Mathematica中的代码:
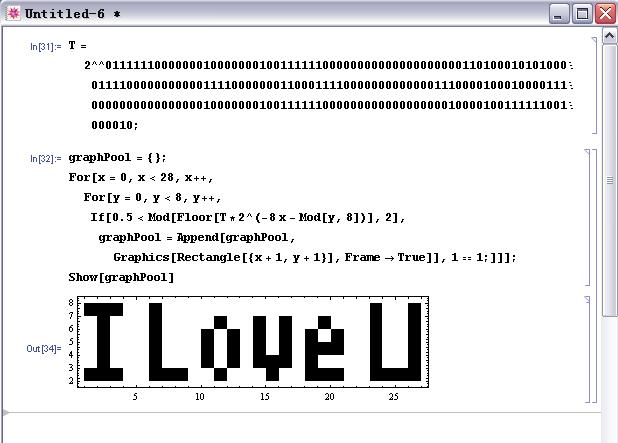
X从0到28,y从0到9变化的过程,也就是从下到上,从左到右描绘出上面的8*28的一个图像了。注意编码的时候是反着的:从上到下,从右到左。
2011年9月28日 12:43
这个不错诶~~呵呵~