每日一题2009/3/29_嵌套平方根
设n为整数,如果式子: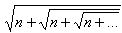 表示一个整数,证明:n为两个连续整数的乘积。
表示一个整数,证明:n为两个连续整数的乘积。
证明:设整数T为式子表示的整数,那么t^2=n+t,即t^2-t-n=0,t=[1+-Sqrt(1-4n)]/2,那么1-4n=r^2,
可以看出r为奇数,所以n=(r^2-1)/4=[(r-1)/2][(r+1)/2],这样就证明了n为两个连续整数的乘积。
设n为整数,如果式子: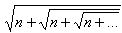 表示一个整数,证明:n为两个连续整数的乘积。
表示一个整数,证明:n为两个连续整数的乘积。
证明:设整数T为式子表示的整数,那么t^2=n+t,即t^2-t-n=0,t=[1+-Sqrt(1-4n)]/2,那么1-4n=r^2,
可以看出r为奇数,所以n=(r^2-1)/4=[(r-1)/2][(r+1)/2],这样就证明了n为两个连续整数的乘积。