还可以这样求和
找出下面和式的化简形式:
n*1+(n-1)*2+(n-2)*3+...+2*(n-1)+1*n=?
(例如:1+2+3+...+n=n(n+1)/2)
解答:我们考虑一个四面体,它每条边上有n个点,包含顶点;假设它的顶点为A,B,C,D,进一步考虑平行于AB和CD的平面和它的截面:第一个就是边AB了,它包含n*1个点,第二个面包含(n-1)*2个点,第三个面包含(n-2)*3个点,继续。。。最后一个也就是CD了,包含1*n个点。像下面这个样子(n=4):
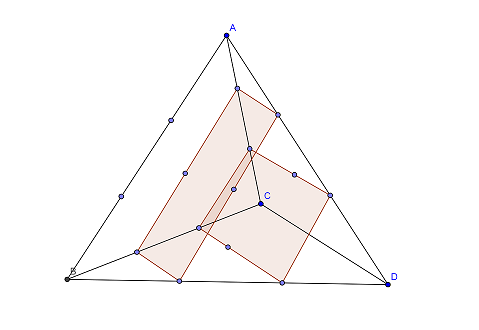
所以我们的式子就等于这个四面体所包含的点数了,这个怎么算了,很容易想到这样子:由于第i层面包含(1+2+3+...+i)=i(i+1)/2个,有n层,这样结果就是Σi(i+1)/2,根据i^2和i的求和公式就可以求出了。
但要是真像这么做了,那这篇文章就完全没意思了。
为了得到总的点数,我们为每个点标记一个三元组:(a,b,c)。a代表所在面的层数,b代表在第几条线上(但是它要从比a大的数开始),c代表在这条线上的第几个位置(也要求从比b大的数开始)。
我们以ABD面为第一层,依次为每个点标记如下:
(1,2,3)
(1,2,4) (1,3,4) (2,3,4)
(1,2,5) (1,3,5) (1,4,5) (2,3,5) (2,4,5) (3,4,5)
(1,2,6) (1,3,6) (1,4,6) (1,4,7) (2,3,6) (2,4,6) (2,5,6) (3,4,6) (3,5,6) (4,5,6)
我们发现这正是从6个数中取3个数的所有取法。怎么看出来的,因为你随便取三个数都可以在其中找到,比如1,3,6。
这样我们的答案就是从n+2个中取3个的取法即:C(n,3)=n(n+1)(n+2)/6。
 评论 (0)
评论 (0)