圆中的面积关系
在一个大圆中,四个半径为大圆一半的小圆过圆心分布在坐标轴的x,y轴正负半轴上,如图:
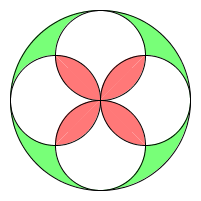
证明小圆两两相交的面积之和(红色区域)和小圆没有覆盖的面积(绿色区域)相等?
先看一个外国人怎么证明的:
证明:先考虑上面图形的1/8,并给各个面积标上a,b,c,d等,如下图:
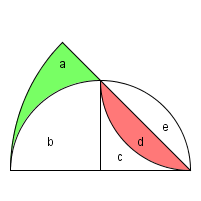
设R是大圆的半径,我们可以得到:
a+b+c+d=PI*R*R/8;
b+c+d+e=PI*R*R/8;
上面的证明也够复杂的,我们一般会这样证明:
证明:设大圆的半径为R,于是我可以得到 S大圆=4*S小圆;
S绿色=S大圆-4*S小圆+S红色;
于是就得S绿色=S红色;
是不是简单多了!
其实按上面的后一种证明方法,可以看出这个结论与四个圆的位置无关,只要它们过大圆圆心且半径为大圆的一半就行了,这时的红色面积就是小圆相交面积的之和,就像下面的两张图片显示的:

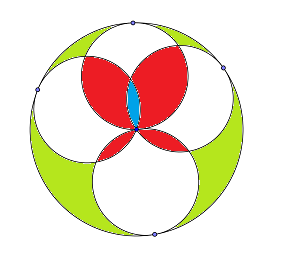
上面的绿色面积都等于相交面积之和。因为绿色面积=大圆面积 - 4*小圆面积+相交面积之和。三个圆相交(上图蓝色)算再次。
 评论 (0)
评论 (0)