Feb 10
n维超立方体的体积很简单,即边s的n次方: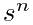 。
。
那n维超球的体积又是怎么样的呢?
首先,我们定义一些概念。圆周是2维圆盘的1维边界(界限)。球面是3维球体的2维表面(界限)。超球面(n维球面)和超球(n维球体)可以有不同的维数。普通的球面是2维球面。普通球体是3维球体。圆周也可以被称为1维球面。圆盘也可以被叫作2维球体。
n维超立方体的体积很简单,即边s的n次方: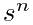 。
。
那n维超球的体积又是怎么样的呢?
首先,我们定义一些概念。圆周是2维圆盘的1维边界(界限)。球面是3维球体的2维表面(界限)。超球面(n维球面)和超球(n维球体)可以有不同的维数。普通的球面是2维球面。普通球体是3维球体。圆周也可以被称为1维球面。圆盘也可以被叫作2维球体。
证明:任给平面上不全共线的n>=3个点,一定存在恰好通过其中两个点的直线。
刚看到这到题的时候还真不知道怎么动手,从两个点开始加点构造,似乎也找不到
明显的规律,看来正面构造是不行的,那反过来构造所有直线都通过至少两个点的情况,
试了半天也找不到,而且也是随着点的增加越来越复杂,怎么办呢?这也难怪解决它花
也许你看过这样的:
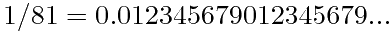
但你不一定看过这样的:
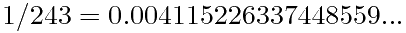
这个系列会怎样继续?243这个数学有什么特别呢?(你可以把它因式分解看看)是什么原因造成这样
的序列的?在其它的基底下有和这个相似的数吗?
首先证明A(n):a,b是使max(a,b)=n成立的任意两个正整数,则a=b.
证明:a)假设A(r)成立;设a,b是任意两个使得max(a,b)=r+1的正整数。
考虑两个整数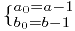 , 则
, 则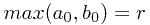 ,又由于我们假设A(r)成立,
,又由于我们假设A(r)成立,
因此  ,由此知
,由此知 。因此A(r+1)成立。
。因此A(r+1)成立。