问：(x - a)(x - b)(x - c)  . . .  (x - z)＝？，给你5秒钟。。。

解答：你一定已经知道了，就是0啦。 (x - a)(x - b)(x - c)  . . .  （x-x)(x-y)(x - z)

           请注意（x-x)，哈哈！！！！

        这是我们学校Dian团队的中国辉老师的一次演讲，觉得很好就贴上来了，很真实，离自己很近。Dian团队主页

钟国辉老师:
        这个题目是我昨天晚上才想好的，我一直觉得这个题目比较难想。刚好最近我也在看《挡不住的趋势》，这本书是刘老师推荐我看的，现在书基本上快看完了，我昨天就想了一下，总不能叫“挡不住的优秀”吧。后来我仔细地思考了一下，我觉得那个题目并不恰当，因为实际上我们的优秀还被阻挡着，所以请大家思考一下：是什么阻挡了我们的优秀？  
正文：
        这个就是我今天要讲的提要，分为四个方面的内容。首先是个引言，接着讨论下我们的核心竞争力在哪里，第三个话题就是我们今天讨论的重点——是什么阻挡了我们的优秀，最后做一个小小的总结，希望我们能从平凡变为优秀，再从优秀回归到平凡。

        博客从2009年4月20号那篇文章之后，就没有再更新了。当初的起因主要是大二下的期中考试，要复习啊，而且今年的5.1正好是考试周，于是5.1就这样考过去了。人总是有懒惰心理的，特别是在紧张之后，考完了总想放松一下，于是博客就放下了。其实要写的东西还是很多的，不过一般也就想想而没有写下来。到6月份，又到了暑期社会实践准备的时候，由于当年大一的时候没去，为了不给大学生活留下遗憾，我也组了个队，这期间也忙了一阵，博客更是没心思管了。但好久不更新博客了，心里也挺过意不去的，于是就有了那篇《博客声明》。暑假前半部分是过着充实而快乐的支教日子（接下来会写），后半部分，先是在家过了一段颓废的日子，超级无聊，到学校，陪同学出去玩，没事看看书，写课程设计。开学了，一直到9月18号，汇编和数字逻辑的课程设计才基本搞定了。这个星期开始就正式上课了，所以博客也要恢复营业了，欢迎大家经常光临。

        博客的内容当然还是主要以数学，计算机知识为主，自己想到的所有东西吧，我还想加入更多自己的大学生活，记录自己的大学生活。博客虽然放在网络上，但是越来越觉得我想要的其实更接近私人化的，虽然我分享自己的想法（上面也用了“营业”这个词），知识，但我并不去刻意让谁去看，看了就接受，你想看就看吧，不喜欢就忽略掉吧。（又不知道在说什么了，想法还没怎么成熟，什么时候做个博客心理学的研究，发现自己对心理学很感兴趣）。

        总之，又要开始写我的博客了，感觉是一个全新的开始，加油，呵呵。。

        记得上学期安装完win7，用起来感觉很爽，后来不知怎么的，发现开始菜单里面，睡眠和休眠按钮都变成灰色了。到电源管理里面查看，发现竟然没有睡眠和休眠的选项了。当时找不到原因，也不知道怎么办，结果一直这样没有睡眠功能用下去。

         这学期一开学，我就重装了win7，到昨天都一切正常的。今天突然发现睡眠又灰了，上网查也没找到什么解决办法。因为最近一在做数字逻辑的课程设计，所以大家机子里都装了isplever这个软件（5.0比较老的软件）。昨天，我一个同学在自己机子上一直生成不了熔丝文件，也没发现什么问题。后来，我发现在我机子上也不能生成熔丝文件，而且错误提示跟在他机子上的一样，但是在学校机房xp系统上都可以正常工作。后来想想他用的是vista系统。于是隐约怀疑睡眠的问题可能也跟isplever有关，后来用powercfg检查，出现下面的结果：

从四月份开始我就没有再更新这个博客了，接下来的一段时间我也不会再更新了。但这决不说明我永远不会更新了。

这其中的原因我会在下个学期开学后公布。

我喜欢这个博客。

我也一直在关注着它。

2009年4月20日会是什么特别的日子呢？说实话今天以前我真的不知道。中午回到寝室看到网站流量爆长，怎么回事 ？原来流量都是从google搜索来的，关键字都和密率，PI，祖冲之有关。于是马上到Google主页，发现Google图标变成这样了：

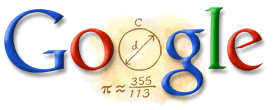
一搜索原来今天是我们中国的PI节：祖冲之诞辰1580年。

井字游戏，英文名是tic-tac-toe，最原始是游戏是在一个3*3的方格棋盘中,每人轮流下看谁先连成横竖或斜着一条线就算赢了，我们把种线叫做tic-tac-toe线，可以在这里http://allaboutfrogs.org/funstuff/java/tictactoe/玩一下这个游戏。现在我们问的是如果是在一个n*n*n的立方体中玩这个游戏，有多少种tic-tac-toe线？比如对于3*3*3的方块，横竖的情况有27种，在面上斜对角的情况有18种，体对角的情况有4种，所以一共有27+18+4＝49种。

解答_证明:

其实这是一道很简单的题，如果用上面的常规做法显然没什么意思，下面看一个另类的做法：