分数维简介
我们平常所听说的维数,或者维数都是对空间的,比如一个点是0维的,一条直线是1维的,一个平面是2维的,一个立体是3维的,这种维数符合庞加莱在1912年提出的维数的拓扑定义,并且——十分合理地——按此定义得到的维数总是整数。但还有一种维数定义,可以得到分数维,也称豪斯道夫-贝斯可维奇维数。这种维数概念最初是由豪斯道夫(Felix Hausdorff)在1919年提出的,并且在后来由贝斯可维奇加以发展,这就是它名字的由来。
分数维是怎样定义的呢?通过对下面标度维数的说明可以体会到分数维数。
我们知道某些形状相同的几何体放在一起可以组成一个较大的它们的复制品。例如,需要2条相同的线段(1维的)组成长度扩大到两倍的一条线段。需要4个相同的正方形(2维几何体)组成棱长扩大到两倍的一个正方形。需要8个相同的正方体组成一个边长扩大到2倍的一个正方体。
为了得到d,也就是维数,可通过对方程两边取对数,这要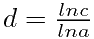 .这样给定c和a就可以求出标度维数d。 这样我们就可以求出各种图形的标度维数了。 例如,康托尔集是把2个相同的部分(c=2)组成长度扩大3倍(a=3)的一个复制品。所以康托尔集的标度维数
.这样给定c和a就可以求出标度维数d。 这样我们就可以求出各种图形的标度维数了。 例如,康托尔集是把2个相同的部分(c=2)组成长度扩大3倍(a=3)的一个复制品。所以康托尔集的标度维数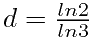 =0.630923...,这是一个实数,但不是整数。
=0.630923...,这是一个实数,但不是整数。

类似的,谢尔宾斯基(Sierpinski)三角形是由三个形状相同(c=3)的图形组成的一个边长扩大到2倍(a=2)的复制品。所以它的标度维数是
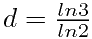 =1.584962...
=1.584962...
对于许多集合,分数维与标度维数是一致的。但分数维对那些不能把相同的几何体放在一起而扩大成复制品的集合仍有定义。分形集合的分数维通常不是一个整数,虽然它有时可以是。例如著名的曼德勃罗特集的边界是分数维就是2,和直线是一样的。

我们到底应该怎样去理解分数维呢?
其实分数维的真正意义在于它能度量“集合充满整个空间的程度“或”集合的粗糙程度“。例如,康托尔集的维数在0和1之间,它充满空间的程度比一个点(0维)大面比直线(1维)小。谢尔宾斯基(Sierpinski)三角形充满空间的程序比直线大比平面图形小。

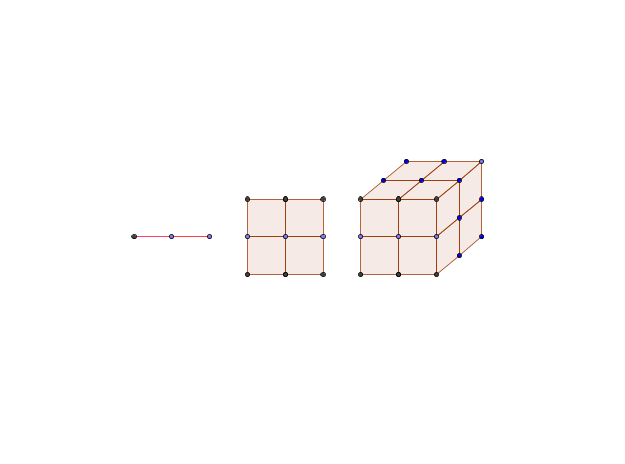
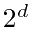 个相同的d维
个相同的d维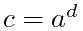 个相同的几何体组成一个边长扩大a倍的大复制品。
个相同的几何体组成一个边长扩大a倍的大复制品。 评论 (0)
评论 (0)