你也许看进球Top 10,音乐Top 100,电影Top 20之类的东西,有想过给数学定理排名吗?
在99年的一次数学大会上有人给出了“百大数学定理”列表,附有定理证明的时间和证明者。
http://personal.stevens.edu/~nkahl/Top100Theorems.html
其中,排名前十位的数学定理如下:
1. 根号2是无理数
2. 代数基本定理
3. 有理数集是可数集
4. 勾股定理
5. 素数定理
6. 歌德尔不完备定理
7. 二次互反律
8. 不可能尺规三等分角和倍立方体
9. 圆的面积
10. 费马小定理的欧拉推广
Mar 17
Mar 10
我今天构造一个这样一个不等式:
0.5 < Mod[Int[T*2^(-8 Int[x] - Mod[Int[y], 8]),2]
其中:T=202486808888363389480137910375037701804044605404484441980698178。
它生成的图像竟然是下面这个样子:
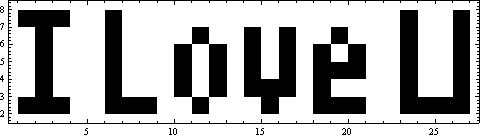
你一定会觉得很神奇,这样的函数是怎么构造出来的呢?仔细想一下,你会发现其实这一点也不难,知道怎么回事后你也可以做出像这样的式子来。
Mar 10
昨天我们上英语课,老师问我们一个问题:如果一个精灵承诺你三个愿望,你会许什么愿望?
有的人说想成为百万富翁,有的人说想变成明星,竟然有一个说想要好多美女做老婆的。
一听到这个问题我就想起了一个搞笑的对上帝不是万能的证明:如果上帝是万能的,那请他创造出一个他自己也举不起来的石头,要是上帝造不出来,显然上帝就是万能的,要是他造出来了,他举不起来,也证明上帝不是万能的。
当老师问到我时,我说:我首先想知道精灵你是否能实现我一切的愿望。
如果他说是,那么我接着说:
我想让你告诉我一个你不能实现的愿望。
如果他说不出,很显然第一个问题你在骗我,如果他真的说出了一个,他还是在骗我。
如果他说不是,那他对我的承诺就是假的。
最后我对老师说,精灵在骗人,他可能不能实现我全部的三个愿望。
我又说,虽然这样,精灵还是可以实现我很多愿望的,既然我至少还有一次机会,我希望精灵再承诺我三个愿望。
老师无语。。。
Mar 6
利用1,3,9克的砝码和一架天平,0到13克整数重量就都可以被称出来了,在下面的Flash中循环显示了这14种重量是怎样被称量的,注意在这个过程中,每一步都只增加或拿下一个砝码。
如果再增加一个27克的砝码,则0到40克的整数重量也都可以被称出来了,存在像上面那样的41步的一个循环吗,它称出所有41种重量,而每一步都只增加或拿下一个砝码?
Feb 28
我相信很多人都已经看过这个问题的,我不久以前看到的,但是自己没能做出来,在网上Cheating了不少解答。
给没看过的朋友介绍一下。
题目要求是只用初等几何知识求出图中的角X:
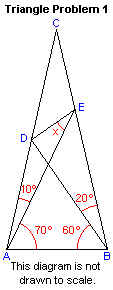
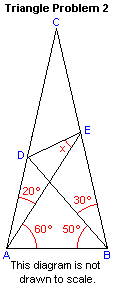
左边这个号称最难,右边这个是第二难的。
Matrix67这里也总结了一些解法:http://www.matrix67.com/blog/archives/382