在数学研究中，我们经常需要寻找一个命题的充分条件。有时候，我们在解题过程中会不自觉地思考结论的充分条件。例如，等底等高便是两个三角形面积相等的充分条件，这就为我们证明三角形面积相等指明了一条道路，接下来我们只需要说明那两个三角形的确是等底等高的就行了。又如，“任意顶点的度数大于等于n/2”是“无向图存在Hamilton回路”的充分条件，它经常被用来说明一个图有Hamilton回路。不过，与寻找必要条件不同的是，寻找一个命题“可以由什么推出来”是一个逆向思维，构造一个充分条件并不容易。有没有一种寻找充分条件的系统方法呢？我最近几天加班加点地研究，终于完成了一个充分条件分析器。你可以在输入框中属于一个与变量x相关的命题，系统将自动给出一个命题的充分条件。这个系统虽然是测试版，但它已经十分强大了。它不仅支持三角函数、对数函数、指数函数、阶乘等各类函数，还支持极限、微分、积分运算，甚至能够处理包括中文在内的自然语言。如果你不知道该输入什么，你可以先点击下面的几个样例试一试。
设n为整数，如果式子：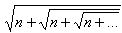
表示一个整数，证明：n为两个连续整数的乘积。
证明：设整数T为式子表示的整数，那么t^2=n+t,即t^2-t-n=0，t=[1+-Sqrt(1-4n)]/2，那么1-4n＝r^2,
可以看出r为奇数，所以n=(r^2-1)/4=[(r-1)/2][(r+1)/2]，这样就证明了n为两个连续整数的乘积。
在提出「生成函数」的数学定义之前，我们先考虑几个简单的排列组合问题。(不知道怎么回事，发表这篇文章首页显示会有问题，搞了好久没找到问题，于是清空重新输入了一遍，并把所有公式都去掉了，用文本代替，首页显示终于没问题了，可能公式就得你费力看了）。
考虑恒等式：(1+ax)(1+bx)(1+cx)=1+(a+b+c)x+(ab+bc+ac)x^2+abcx^3
如将a,b,c 看作代表三个对象，它的右边是一多项式，其系数恰代表了将 a,b,c 作组合的各种可能。常数项1表示在三对象中一个都不取；x 的系数a+b+c 表示在a,b,c 中取一个的各种组合，即或取a，或取b，或取 c；x^2 的系数ab+bc+ac 表取二个的各种组合；x^3之系数表示了三个皆取的唯一方法。在这里可能产生各种情形是用+号连接，同时发生之事件则用乘法（即符号并列）表示。
又设有5个球 a,a,a,b,c，其中三个球a 完全一样，则恒等式：
(1+ax+a^2x^2+a^3x^3)(1+bx)(1+cx)= 1+(a+b+c) x+(a^2+a b+a c+b c) x^2+(a^3+a^2 b+a^2c+
a b c) x^3+(a^3 b+a^3 c+a^2 b c) x^4+a^3 b c x^5
其中 x^r的系数表示了选取r个的各种可能组合(1<=r<=5 )。
在排列组合问题中，加法原则与乘法原则是大家熟知的两个法则。加法原则是讲如一事件可能发生情况有 m 种，另一种事件可能发生情况有 n 种，则这两种事件其一发生情况有m+n 种。乘法原则是讲如一事件可能发生情况有m种，另一事件可能发生情况有n种，则这两事件同时发生情况有mn种。我们在上面两例用到的是一种符号运算，它遵从这两法则。在第二个例子中，因子(1+ax+a^2x^2+a^3x^3)表示了或不取a，或取一个a，或取2个a，或取三个a 的各种情况；而在第一个例子中，(1+ax)(1+bx)表示了如果 a , b 被允许同时选取时可能产生之各种情况。
能否找到五个连续的整数，使前面的四个数的四次方之和等于最后一个数的四次方？
解答：也许你用Mathematica算出很长一个表达式，显然不是整数。事实确实是找不到，证明很简单：我们考虑下一个数的四次方被5除的余数，可以只看这几个数5k,5k+1,5k+2,5k+3,5k+4,可以看出余数分别是0,1,1,1,1。这样当把前前4个余数起来只能是3或4,这样就证明了无解了。
